
NOEL CHALMERS
MTS Design Engineer @ AMD Research
Currently working at AMD Research. While at VT he worked on a project funded in part by the Department of Energy Center for Efficient Exascale Discretizations.
His research interests include high-order continuous and discontinuous finite element methods, incompressible flows, preconditioning strategies, and parallel/algebraic multigrid methods.
RESULTS GALLERY

Full publication list on scholar.google.
RECENT MANUSCRIPTS
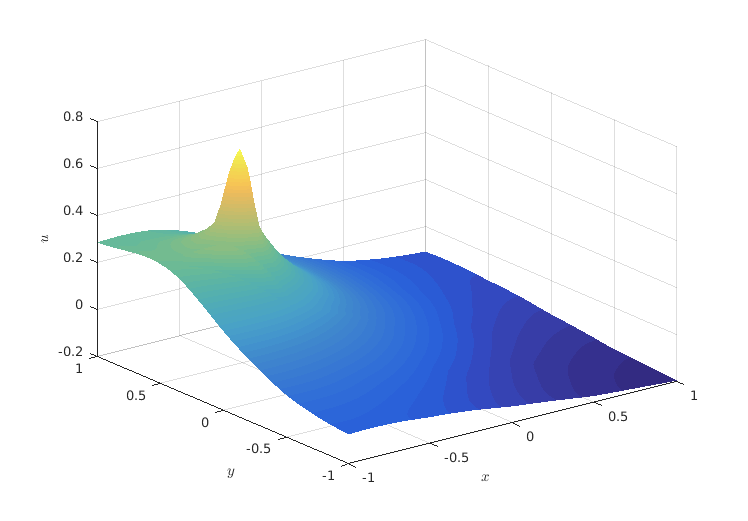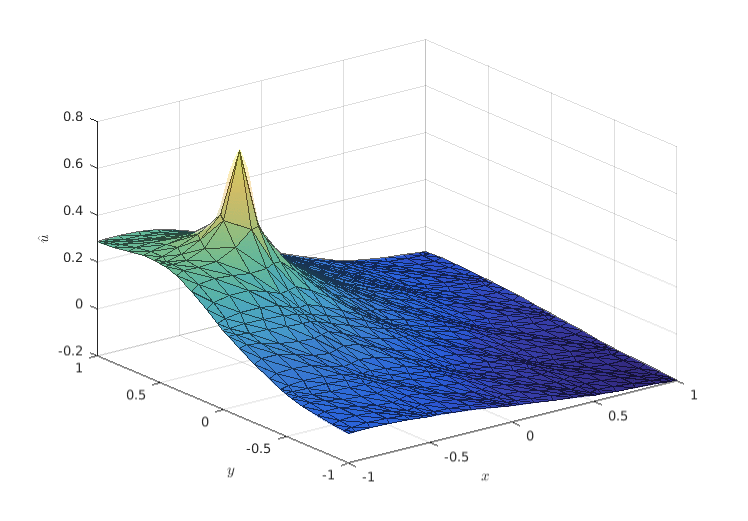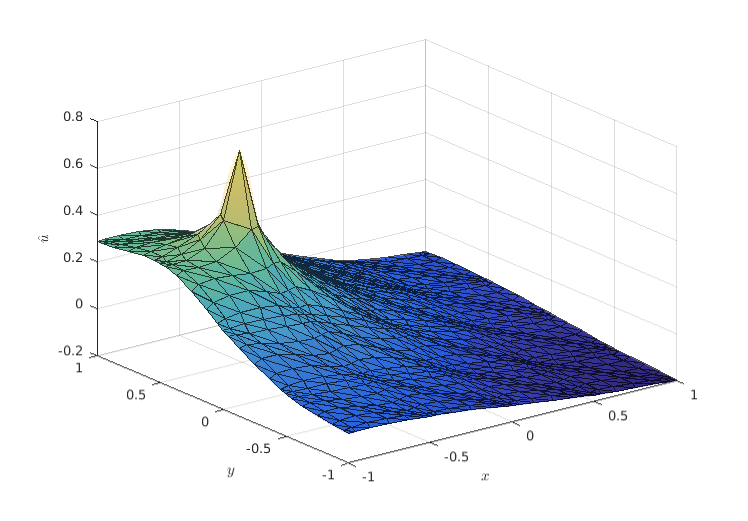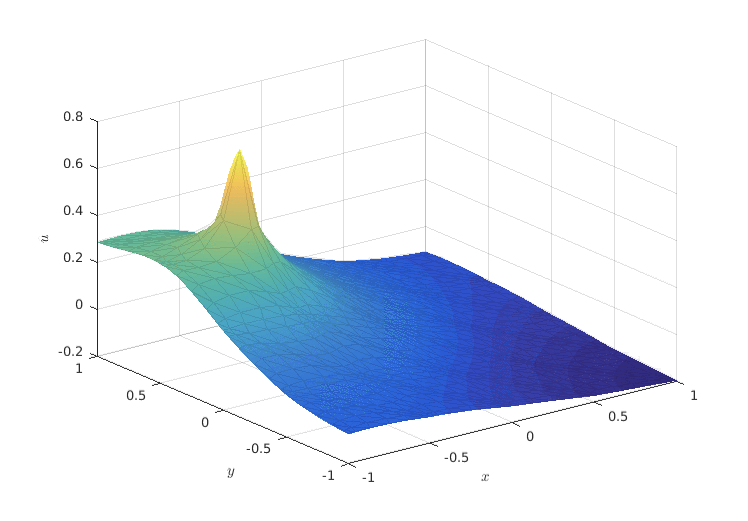
LOW-ORDER PRECONDITIONING OF HIGH-ORDER TRIANGULAR FINITE ELEMENTS
October 2017
Authors: Noel Chalmers and Tim Warburton
Status: Submitted to SIAM Journal on Scientific Computing
Abstract: We propose a new formulation of a low-order elliptic preconditioner for high-order triangular elements. In the preconditioner, the nodes of the low-order finite element problem do not necessarily coincide with the high-order nodes. Instead, the two spaces are connected using least squares projection operators. The effectiveness of the preconditioner is demonstrated to be highly sensitive to the location and number of vertices used to construct the low-order finite element mesh on each high-order element. We treat the number of low-order vertices and their locations as optimizable quantities and chose them to minimize the condition number of the preconditioned stiffness matrix on the reference element. We present computational results that demonstrate that the condition number of the preconditioned high-order stiffness matrix on the reference element can be improved. The best performing preconditioners are formed with low-order finite element meshes that have more vertices than the high-order element has degrees of freedom, and have nodes grouped close to the element edges.

A ROBUST CFL CONDITION FOR THE DISCONTINUOUS GALERKIN METHOD ON TRIANGULAR MESHES
January 2017
Authors: Noel Chalmers and Lilia Krivodonova
Status: Submitted to Journal of Computational Physics
Abstract: When the discontinuous Galerkin (DG) method is applied to hyperbolic problems in two dimensions on triangular meshes and paired with an explicit time integration scheme, an exact CFL condition is not known. The stability condition which is most usually implemented involves scaling the time step by the smallest radius of the inscribed circle in every cell. However, this is known to not provide a tight bound on the largest possible stable time step in some cases. In this paper, we apply the DG method to a simple linear problem and derive a
PDE which is satisfied by the numerical solution itself. By applying classical Fourier analysis to the solutions of this PDE we find a natural scaling of the spectrum of the DG spatial operator by a parameter hj , which can be seen to be the width of the cell Ωj along the characteristic direction of flow. We use this parameter to propose a new CFL condition and show through several numerical examples that we are able to select significantly larger time steps than usually obtained using the inscribed radii of the computational cells.
